Auf dieser Seite finden Sie Rätsel, Späße, Spiele, Nachdenkenswertes. Bei der einen oder anderen Aufgabe werden auch Mathematiker ins Grübeln kommen. Ich wünsche gute Unterhaltung.
Jeden Monat erhält der fünfte Einsender einer Lösung irgendeiner der Aufgaben eine kleine Überraschung.
Ein Bauer hat 17 Hühner. Alle außer 9 holt nachts der Fuchs.
Wie viele Hühner bleiben übrig?
Eine halbe Glatze hat 30000 Haare.
Wieviele Haare hat eine ganze Glatze?
Wenn ich mit Ihnen wetten würde, dass die nächste Person, die Sie erblicken,
mehr Arme hat als der Durchschnitt der Bevölkerung,
würde ich meistens diese Wette gewinnen.
Warum ist das so?
In einer Gerichtsverhandlung in Erbschaftsangelegenheiten,
die im Jahre 2017 stattfand, sagte ein Zeuge aus,
dass sein leiblicher Bruder im Jahre 1889 verstorben sei.
Der Richter ermahnte ihn, sich vor Gericht keine Scherze zu erlauben,
doch der Zeuge beharrte auf seiner Aussage.
Wie kann es sein, dass der Zeuge die Wahrheit gesagt hat?
Beschränktes Wachstum |
Drei Gäste bezahlten zusammen 30 € für eine Familienpizza, 10 € pro Person.
Nachdem sie gegangen waren, fiel dem Wirt auf,
dass er ihnen nur eine Pizza für 25 € serviert hatte und
weil der Wirt ein ehrlicher Mensch war,
schickte er seinen Azubi los, um den Gästen 5 € zurück zu geben.
Der Azubi wusste nicht, wie er 5 € an drei Personen verteilen sollte,
deshalb behielt er 2 € für sich und gab jedem Gast 1 €.
Es ist doch eigenartig:
Die Gäste bezahlten jeder 10 € – 1 € = 9 €, also zusammen 27 €.
Der Azubi hat 2 € behalten, das macht zusammen 29 €.
Der Wirt hat aber 30 € bekommen.
Was ist aus dem einen Euro geworden?
Die Eierfrau auf dem Markt sagt, sie habe heute schon gute Geschäfte gemacht.
Ihr erster Kunde, ein Kantinenkoch, habe die Hälfte der Eier gekauft,
die sie dabei hatte, plus ein halbes Ei,
der zweite Kunde, ein Bäckermeister,
habe die Hälfte der restlichen Eier gekauft plus ein halbes Ei,
der dritte Kunde wieder die Hälfte des Restes plus ein halbes Ei
und so weiter.
Bisher habe sie auf diese Art acht Kunden bedient und nur noch ein Ei übrig.
Wie kann es sein, dass sie die Wahrheit gesagt
und trotzdem kein Ei halbiert hat?
Ein Bärenjäger geht morgens von seinem Zelt aus zehn Meilen genau nach Süden.
Dann trifft er einen Bären, den er zehn Meilen genau nach Westen verfolgt.
Nach zehn Meilen biegt der Bär ab und der Jäger verfolgt
ihn weitere zehn Meilen genau nach Norden.
Da stellt er fest, dass er sich wieder genau an seinem Zelt befindet.
Welche Farbe hat der Bär?
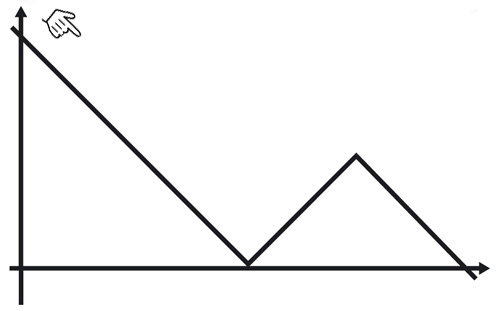
Schaubild einer nicht überall differenzierbaren Funktion |
Kann man ein Schachbrett, aus dem zwei diagonal gegenüberliegende
Eckfelder herausgeschnitten sind, vollständig mit Dominosteinen überdecken,
sodass ein Dominostein immer zwei nebeneinanderliegende Felder bedeckt?
Gedankenlesen:
Schreibe die Ziffern von 1 bis 9 auf jeweils ein Kärtchen.
Du kannst die neun Kärtchen ergänzen durch einige weitere Kärtchen,
auf die du jeweils eine 0 schreibst.
Bitte jemanden,
aus all diesen Kärtchen beliebige Zahlen zu bilden.
Er muss alle Kärtchen verwenden.
Die Ziffern 1 bis 9 kommen also in den entstandenen Zahlen jeweils
genau einmal vor und zusätzlich gibt es eventuell noch Nullen.
Er soll alle diese Zahlen addieren, von der Summe
eine beliebige Ziffer, die nicht Null ist, durch ein X ersetzen und dir das Ergebnis zeigen.
Du kannst sagen, für welche Ziffer das X steht!
Bilde dazu die Quersumme der Zahl, die dein Mitspieler dir mitgeteilt hat.
An der Stelle, wo jetzt das X steht, stand die Ziffer,
die die Quersumme zu einer Zahl aus der Neunerreihe ergänzen würde.
Beispiel:
190 + 23 + 405 + 700 + 60 + 8 = 1386
Dein Mitspieler zeigt dir: 13X6
1 + 3 + 6 = 10
Die nächste Zahl aus der Neunerreihe ist 18, also fehlt die 18 - 10 = 8 an der Stelle von X.
Bitte nur einmal lesen und dann sofort nacherzählen:
Ein Zweibein saß auf einem Dreibein und verzehrte ein Einbein.
Es kam ein Vierbein und nahm dem Zweibein das Einbein weg.
Da nahm das Zweibein das Dreibein und schlug das Vierbein.
Wenn es noch nicht so richtig geklappt hat, lies die Geschichte nochmals
und versuche Dir dabei etwas vorzustellen. Jetzt klappt es plötzlich.
Liebe Schülerinnen und Schüler, Ihr stöhnt doch oft, dass Ihr
so viel Zeit für die Schule aufwenden müsst, aber stimmt das denn überhaupt?
Wenn Ihr jeden Tag acht Stunden schlaft, dann sind das umgerechnet 122 Tage im Jahr.
Es bleiben noch 365 - 122 = 243 Tage.
Für Körperpflege, Essen usw. braucht Ihr 90 Minuten pro Tag, das sind 23 Tage im Jahr.
Es bleiben also 243 - 23 = 220 Tage.
Für den Schulweg und die Pausen braucht Ihr auch 90 Minuten pro Tag, 23 Tage pro Jahr.
Es bleiben 220 - 23 = 197 Tage.
Zieht man davon die Samstage und Sonntage ab, so bleiben noch 197 - 52 - 52 = 93 Tage.
Und die reichen ja noch nicht einmal für die Ferien.
Wann geht Ihr eigentlich überhaupt zur Schule???
Wenn du von 3 Äpfeln 2 wegnimmst, wie viele Äpfel hast du dann?
Nachhilfe bei Juristen:
Ein Rechtsanwalt hilft einem Jurastudenten beim Studium.
Sie vereinbaren, dass der Student dem Rechtsanwalt nur dann
ein Honorar zahlen muss, wenn er seinen ersten Gerichtsprozess gewinnt.
Nach Ende seiner Ausbildung führt der frischgebackene
Jurist aber gar keinen Gerichtsprozess.
Der Lehrer möchte sein Honorar bekommen, droht, ihn zu verklagen und sagt:
Du musst mir mein Honorar auf jeden Fall zahlen.
Wenn du den Prozess gewinnst, musst du zahlen,
weil es so vereinbart war, dass du zahlen musst, wenn du deinen ersten Prozess gewinnst.
Wenn du ihn verlierst, musst du zahlen,
weil dich dann ja das Gericht dazu verurteilt zu zahlen.
Der ehemalige Student sagt:
Ich muss auf keinen Fall zahlen.
Wenn ich den Prozess verliere,
muss ich nicht zahlen, weil es zwischen uns so vereinbart war.
Gewinne ich aber, dann muss ich nicht zahlen, weil das Gericht es so bestimmt hat.
Da hat doch jemand vergessen, eine Flasche mit Saft zu verschließen
und ein Teil des Wassers ist verdunstet. Vorher war der Wassergehalt des Saftes 99 %,
nach der Verdunstung war er nur noch 98 %.
Wenn der Saft vorher 1 kg gewogen hat, was wiegt er hinterher?
Hoffentlich sehen Sie Mathematik nicht so:
„Was er sah, war sinnverwirrend. In einer krausen, kindlich dick aufgetragenen Schrift bedeckte ein phantastischer Hokuspokus, ein Hexensabbat verschränkter Runen die Seiten. Griechische Schriftzeichen waren mit lateinischen und mit Ziffern in verschiedener Höhe verkoppelt, mit Kreuzen und Strichen durchsetzt, ober- und unterhalb waagrechter Linien bruchartig aufgereiht, durch andere Linien zeltartig überdacht, durch Doppelstrichelchen gleichgewertet, durch runde Klammern zu großen Formelmassen vereinigt. Einzelne Buchstaben, wie Schildwachen vorgeschoben, waren rechts oberhalb der umklammerten Gruppen ausgesetzt. Kabbalistische Male, vollständig unverständlich dem Laiensinn, umfassten mit ihren Armen Buchstaben und Zahlen, während Zahlenbrüche ihnen voranstanden und Zahlen und Buchstaben ihnen zu Häupten und Füßen schwebten. Sonderbare Silben, Abkürzungen geheimnisvoller Worte, waren überall eingestreut, und zwischen den nekromantischen Kolonnen standen geschriebene Sätze und Bemerkungen in täglicher Sprache, deren Sinn gleichwohl so hoch über allen menschlichen Dingen war, dass man sie lesen konnte, ohne mehr davon zu verstehen als von einem Zaubergemurmel.“
(Aus „Königliche Hoheit“ von Thomas Mann.)
|
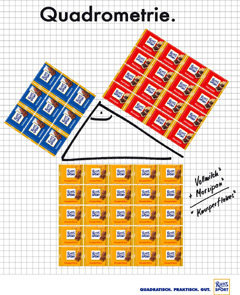
Die Firma Ritter stellt in Waldenbuch Schokolade her und bevorzugt die Quadratform.
|
Eine kleine lustige Korrespondenz, die ich mit der Firma Ritter geführt habe:
|
Sehr geehrte Damen und Herren,
als Nachhilfelehrerin für Mathematik ziehe ich häufiger Gegenstände meines Haushaltes heran, um mathematische Sachverhalte anschaulich zu machen. In dem Buch von Peter Baptist „Pythagoras und kein Ende?“ fand ich Ihre nützliche Werbung Quadrometrie, die ich gerne benutze, um den Satz des Pythagoras zu erklären. Mir ist jedoch mit einem Schüler der 6. Klasse ein böses Missgeschick passiert. Als ich zur Berechnung der Würfeloberfläche ein Anschauungsobjekt brauchte, fiel mir eine Packung Ritter Sport Schokowürfel ins Auge. Ich gab dem Schüler die geschlossene Packung mit der Anweisung, er solle schon mal einen Würfel herausnehmen, messen und rechnen, während ich noch andere Dinge erledigte. Als ich wiederkam, fand ich einen völlig verstörten Schüler vor, der mir sagte, er könne die Seite „a“ nicht messen, weil er nicht wisse, welche das sei. Erschreckt stellte ich fest, dass ich dem armen Schüler zur Berechnung der Würfeloberfläche einen Pyramidenstumpf zur Anschauung gegeben hatte. Dieser Schüler wird in Zukunft kein Vertrauen mehr zu mir haben. Wenn er das tragische Vorkommnis gar in seiner Schule weitererzählt, ist mein Ruf als Lehrerin ruiniert und meine Existenzgrundlage ist mir entzogen. Damit Sie nicht weiter zur Verwirrung der Jugend und zum Ruin der Lehrer beitragen, ersuche ich Sie, entweder Ihre Schokowürfel korrekterweise in Schokopyramidenstümpfe umzubenennen oder aber in Zukunft in Würfelform zu produzieren. Mit freundlichen Grüßen Merle Porta |
Sehr geehrte Frau Porta,
wir bedanken uns für Ihr Schreiben und Ihre kritischen Anmerkungen zum Thema Schoko„würfel“. Selbstverständlich haben Sie Recht. Rein geometrisch gesehen handelt es sich bei den Schokowürfeln nicht um Würfel, da die Kantenlängen nicht die gleichen Abmessungen besitzen. Für Sie als Mathematikerin mag das etwas befremdlich wirken, allerdings spielen bei der Wahl der Produktbezeichnung eines Artikels auch andere, vielleicht weniger mathematisch-wissenschaftliche Gesichtspunkte eine Rolle. So es ist aus produktionstechnischer Sicht von entscheidendem Vorteil, wenn das Produkt keine senkrechten Seitenflächen hat. Nach dem Gießen und Abkühlen der Produkte zieht sich der Schokoladenkörper ganz wenig zusammen und kann bei konisch zulaufender Form problemlos aus der Gießform gelöst werden. Bei senkrechten Seitenflächen müsste man die Hülle aus zwei Teilen fertigen oder den Schokoüberzug nachträglich aufbringen. Aus verkaufs- und marketingpolitischen Gründen ist andererseits die Bezeichnung „Schokowürfel“ vorteilhafter, da es wohl dem „normalen“ Verbraucher nicht unbedingt klar ist, um was es sich bei einem Produkt handelt, das „Schokopyramidenstümpfe“ heißt. Nicht zuletzt haben die einzelnen „Würfel“ ungefähr die gleiche Form wie einzelne Stückchen der bekannten 100g-Tafel und besitzen damit so etwas wie einen „Wiedererkennungswert“. Wir sind sicher, dass Sie das Vertrauen des Schülers durch geeignete pädagogische Maßnahmen wieder gewinnen werden und dass Ihr Ansehen als Mathematikerin nicht dauerhaft beschädigt sein wird. Als kleine Wiedergutmachung für die entstandenene „Rufschädigung“ erlauben wir uns, ohne Anerkennung einer rechtlichen Pflicht, Ihnen in den nächsten Tagen ein kleines Schokopäckchen mit getrennter Post zukommen zu lassen. Die Umverpackung kann im Übrigen relativ gefahrlos zur Berechnung eines Quadervolumens herangezogen werden. Die Berechung der einzelnen Tafelvolumina sollte dagegen Bestandteil höherer Leistungsklassen sein. |
Der sieht nicht nur aus wie sein eigener Großvater, er ist es tatsächlich ...
Herr Müller heiratete eine Witwe, die eine erwachsene Tochter hatte.
Der Vater von Herrn Müller verliebte sich bei der Hochzeit in die Stieftochter
seines Sohnes und heiratete sie.
Nun war der Vater von Herrn Müller gleichzeitig sein Schwiegersohn,
während seine Stieftochter auch seine Stiefmutter wurde, denn sie war ja die Frau seines Vaters.
Ein Jahr nach der Hochzeit bekam die Frau von Herrn Müller eine Tochter,
die war Schwägerin des Vaters von Herrn Müller, denn sie war ja die Schwester seiner Frau.
Die Tochter von Herrn Müller war auch seine Tante,
denn sie war die Schwester seiner Schwiegermutter, also der Frau seines Vaters,
die die Tochter seiner Frau war.
Im Jahr danach bekam die Stieftochter von Herrn Müller,
die die Frau seines Vaters, also seine Stiefmutter war, einen Sohn.
Der war (als Sohn des Vaters von Herrn Müller) Bruder von Herrn Müller und
(als Sohn der Tochter seiner Frau) sein Enkelkind.
Die Frau von Herrn Müller wurde seine Großmutter, denn Sie war Großmutter seines Bruders.
Als Mann seiner Großmutter war Herr Müller also sein eigener Großvater.